Equazione di Eyring: dimostrazione, usi
L’equazione di Eyring è dovuta al chimico messicano naturalizzato statunitense Henry Eyring che ha dato un notevole contributo allo studio della cinetica delle reazioni. L’equazione di Eyring è un’equazione utilizzata nella cinetica chimica per descrivere i cambiamenti di velocità con la temperatura
Consideriamo la reazione di equilibrio A + B ⇄ C per la quale la costante di equilibrio K è pari a:
K = [C]/[A][B]
La variazione di energia libera allo stato standard è correlata alla costante di equilibrio dall’equazione:
ΔG° = – RT ln K
Dove R è la costante universale dei gas pari a 8.31 J K-1 mol-1 e T è la temperatura in gradi Kelvin. Poiché ΔG° = ΔH° – T ΔS°
Allora si ha: ΔH° – T ΔS°= – RT ln K
Dividendo ambo i membri per – RT si ha:
– ΔH°/ RT + ΔS°/ R = ln K
Costante di equilibrio e temperatura
Da cui si evince che ln K è inversamente proporzionale a 1/T; tale relazione sviluppata da vant’Hoff nella sua equazione mostra una dipendenza della costante di equilibrio dalla temperatura infatti la costante di un equilibrio è costante solo a temperatura costante.
Anche la velocità di una reazione varia con la temperatura: all’aumentare della temperatura la velocità di una reazione aumenta.
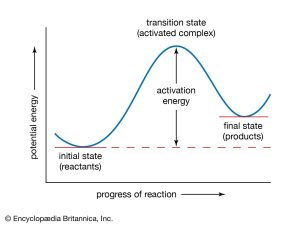
Secondo la teoria dello stato di transizione la velocità di una reazione è determinata dalla formazione di uno stato del sistema reagente, detto stato di transizione o complesso attivato che soddisfi i requisiti di una collisione efficace. Lo stato di transizione è un aggregato molecolare in cui le molecole reagenti con sufficiente energia hanno dato luogo a un urto efficace a seguito del quale si trovano nelle condizioni di dare i prodotti di reazione.
L’equazione di Eyring si basa sulla teoria dello stato di transizione ed è usata per descrivere la relazione tra la velocità di reazione e la temperatura. L’equazione di Eyring è analoga all’equazione di Arrhenius ma l’equazione di Arrhenius può essere applicata solo a sistemi allo stato gassoso mentre l’equazione di Eyring estende il campo a reazioni che avvengono in fase condensata.
L’espressione dell’equazione di Eyring, che fornisce un calcolo più preciso delle costanti di velocità e permette di comprendere il progresso di una reazione a livello molecolare è data da:
k = kBT / h e-ΔH±/RT e ΔS±/T
dove kB è la costante di Boltzmann, h è la costante di Planck, ΔH± e ΔS± sono rispettivamente la variazione di entalpia e di entropia del complesso attivato.
Dimostrazione
Consideriamo nuovamente la reazione A + B ⇄ C e supponiamo che proceda con la formazione del complesso attivato AB±:
A + B ⇄ AB± ⇄ C
La costante K± relativa all’equilibrio di formazione di AB± è data da:
K± = [AB±]/[A][B] (1)
Lo stato di transizione AB± è poco stabile e presenta il massimo dell’energia: solo quando questo massimo di energia viene raggiunto la reazione procede verso la formazione dei prodotti
La velocità della reazione è uguale al numero di complessi attivati che si decompongono per dare i prodotti ovvero:
velocità = v [AB±] (2)
dove v è la frequenza di vibrazione
Poiché dalla (1) K± [A][B] = [AB±]
Sostituendo nella (2) a [AB±] il suo valore si ha:
velocità = v K± [A][B] (3)
La velocità della reazione può essere espressa come:
v = k [A][B]
da cui k [A][B] = v K± [A][B]
ovvero k = v K±
Poiché la frequenza di vibrazione v è data da v = kBT/h allora
k = kBT K±/h
 Poiché – ΔH±/ RT + ΔS±/ T = ln K±
Poiché – ΔH±/ RT + ΔS±/ T = ln K±
Allora k = kBT / h e-ΔH±/RT e ΔS±/T
Riportando in grafico ln k/T contro 1/T si ottiene una retta con coefficiente angolare – ΔH±/R da cui si ricava l’entalpia di attivazione e intercetta ln kB/h + ΔS±/R che fornisce l’entropia di attivazione



