Costante di reticolo
La costante di reticolo è un valore che descrive la spaziatura tra celle unitarie adiacenti in una struttura cristallina. La costante di reticolo, unitamente alle lunghezze dei bordi delle celle unitarie e agli angoli piani sono parametri importanti delle strutture periodiche dei materiali cristallini. La previsione della costante del reticolo cristallino ha ampie applicazioni nella previsione della struttura cristallina e nella previsione delle proprietà dei materiali.
La costante di reticolo di cristalli grandi, chimicamente puri e altamente perfetti può essere misurata con tecniche di diffrazione di raggi X ad alta precisione. Il reticolo di Bravais, dal nome del matematico Auguste Bravais, elemento base da cui possono essere costruiti tutti i cristalli, è un insieme infinito di punti discreti aventi disposizione geometrica sempre uguale in tutto lo spazio.
Questi reticoli rientrano in sette diversi sistemi cristallini, che si differenziano dalla relazione tra gli angoli tra i lati della cella unitaria e la distanza tra i punti nella cella unitaria. La cella unitaria è il più piccolo gruppo di atomi, ioni o molecole che, se ripetuto a intervalli regolari in tre dimensioni, produrrà il reticolo di un sistema cristallino. La costante di reticolo è la lunghezza tra due punti sugli angoli di una cella unitaria. Ciascuna delle varie costanti di reticolo è indicata dalle lettere a, b e c.
Legge di Bragg e costante di reticolo
Quando un cristallo viene bombardato con raggi X di una lunghezza d’onda dello stesso ordine di grandezza della spaziatura dei piani del reticolo cristallino su scala atomica e a determinati angoli di incidenza, vengono prodotti intensi raggi X riflessi quando le lunghezze d’onda dei raggi X dispersi interferiscono costruttivamente.
Affinché le onde possano interferire in modo costruttivo, le differenze nel percorso devono essere pari a multipli interi della lunghezza d’onda. Quando si verifica questa interferenza costruttiva, un fascio diffratto di raggi X lascerà il cristallo con un angolo uguale a quello del fascio incidente.
La relazione generale tra la lunghezza d’onda dei raggi X incidenti, l’angolo di incidenza e la spaziatura tra i piani del reticolo cristallino degli atomi è nota come Legge di Bragg, proposta per la prima volta da William Lawrence Bragg e suo padre, William Henry Bragg , nel 1913 espressa come:
nλ = 2 d sen Θ (1)
dove n è un numero intero che rappresenta l’ordine di riflessione, λ è la lunghezza d’onda dei raggi X incidenti, d è la spaziatura interplanare del cristallo e Θ è l’angolo di incidenza. Nel reticolo cristallino di NaCl i piani si trovano paralleli alle superfici delle celle unitarie del cristallo.
La loro distanza d corrisponde alla metà della costante di reticolo a0:
d = a0/2 (2)
Sostituendo nella (1) a d il valore della (2) si ottiene:
nλ = 2 d sen Θ = 2 (a0/2) sen Θ = a0 sen Θ
da cui la costante di reticolo a0 è data da nλ/senΘ
Sistema cubico e costante di reticolo
La struttura di un solido cristallino è descritta considerando la sua unità ripetitiva più semplice, chiamata cella unitaria. La cella unitaria è costituita da punti reticolari che rappresentano le posizioni degli atomi o degli ioni e l’intera struttura è quindi costituita dalla cella unitaria che si ripete in tre dimensioni.
Gli studi cristallografici hanno mostrato che sono necessari solamente sette diversi sistemi cristallini per dare origine a tutti i possibili tipi di reticolo ovvero il sistema cubico, tetragonale, rombico, monoclino, triclino, trigonale e esagonale.
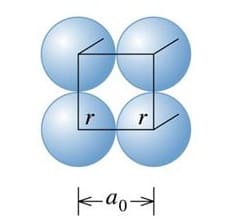
Una cella unitaria cubica genera tre reticoli di Bravais ovvero il reticolo cubico semplice, reticolo cubico a corpo centrato (BCC) e reticolo cubico a facce centrate (FCC). Nel reticolo cubico semplice detto anche cella primitiva la cella unitaria è costituita da un cubo ai cui vertici vi sono 8 atomi, molecole o ioni, assimilati a sfere, presenti ai vertici sono condivise con 8 celle unitarie adiacenti si può ritenere che solo 1/8 di ogni sfera appartenga ad una data cella unitaria. Poiché ci sono otto angoli il numero di sfere per ogni cella unitaria è pari a (8∙ 1/8) = 1.
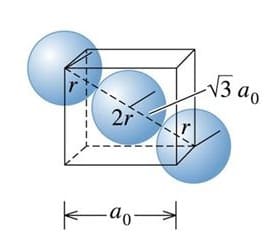
La cella unitaria di un reticolo cubico a corpo centrato (BCC) è costituita da un cubo ai cui vertici vi sono 8 atomi, molecole o ioni e uno al centro. La sfera centrale è circondata da 8 sfere quindi il numero di coordinazione ovvero il numero di sfere con i quali una data sfera è in contatto è pari a 8. Poiché le sfere presenti ai vertici sono condivise con 8 celle unitarie adiacenti si può ritenere che solo 1/8 di ogni sfera appartenga ad una data cella unitaria.
Quindi le otto sfere presenti ai vertici nel loro insieme contribuiscono nel loro insieme all’equivalente di una sfera pertanto il numero di sfere per ogni cella unitaria è pari a 1+ (8∙ 1/8) = 2.
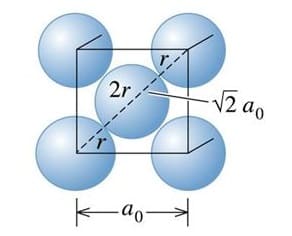
La cella unitaria di un reticolo cubico a facce centrate (FCC) è costituita da un cubo ai cui vertici vi sono 8 atomi, molecole o ioni e uno al centro di ogni faccia del cubo. Le otto sfere presenti ai vertici nel loro insieme contribuiscono nel loro insieme all’equivalente di una sfera mentre le sei sfere presenti sulle facce del cubo contribuiscono nel loro insieme all’equivalente di 6/2= 3 pertanto il numero di sfere per ogni cella unitaria è pari 3+1 = 4.
La geometria di una cella unitaria è determinata da un insieme di valori numerici chiamati parametri reticolari o costanti reticolari. In linea teorica il numero massimo di parametri del reticolo è pari a 6 in quanto vi sono tre angoli e tre direzioni spaziali. Tuttavia, le simmetrie riducono tale numero in molti casi. Per una cella cubica, infatti, gli angoli sono già definiti, tutti uguali 90°
Allo stesso modo, i tre parametri reticolari spaziali sono uguali tra loro: questo ci lascia con un’unica costante di reticolo a0. L’unica variabile nella determinazione della costante di reticolo è il raggio atomico R delle specie che compongono il cristallo.
Da banali considerazioni di tipo geometrico per un reticolo cubico semplice la costante di reticolo a0 è pari a: a0 = 2 R
Nel caso di un reticolo cubico a corpo centrato la costante di reticolo a0 è pari a: a0 = 4 R/√3 mentre in un reticolo cubico a facce centrate la costante di reticolo a0 è pari a: a0 = 2√2 R.



