Modi vibrazionali
I modi vibrazionali descrivono una serie di proprietà, come la dipendenza dalla temperatura dei parametri del reticolo cristallino e delle costanti elastiche e determinano le proprietà di espansione termica, conducibilità termica ed elettrica, funzioni termodinamiche e posizione della temperatura critica nei diagrammi di fase.
Gli atomi che costituiscono una molecola non sono immobili, ma oscillano attorno alla loro posizione di equilibrio. Queste oscillazioni, chiamate modi vibrazionali, sono raggruppate in base a come modificano la geometria molecolare.
Il numero di possibili modi vibrazionali dipende dall’esatta geometria molecolare e dal numero di atomi nella molecola. Allo stesso tempo, le molecole possono anche ruotare attorno ai propri assi di simmetria. Nella meccanica quantistica, queste vibrazioni e rotazioni sono quantizzate, cioè gli atomi possono oscillare o ruotare solo a frequenze molto specifiche e tali frequenze sono caratterizzate da numeri quantici.
Gli stati quantistici vibrazionali sono generalmente indicati con v e gli stati quantistici rotazionali generalmente da J . Per passare da un certo stato a uno superiore, la molecola ha bisogno di assorbire un fotone con energia quantizzata e, viceversa, per passare ad uno stato inferiore la molecola emetterà tale fotone.
Per gli stati vibrazionali, le energie dei fotoni cadono tipicamente nella regione dell’infrarosso mentre per gli stati rotazionali puri, le energie dei fotoni sono molto più basse e tipicamente si trovano nella regione delle microonde dello spettro elettromagnetico della luce. Poiché le proprietà rotazionali dipendono tuttavia dalla geometria, ogni stato vibrazionale ha il proprio insieme di stati rotazionali.
Numero dei modi vibrazionali
Con il termine grado di libertà si indica il numero di modi in cui una molecola nella fase gassosa può muoversi, ruotare o vibrare nello spazio. Il concetto di grado di libertà fu introdotto dal matematico tedesco Carl Friedrich Gauss nelle sue opere all’inizio del 1821. Il grado di libertà è quindi il numero di variabili necessarie per descrivere completamente il movimento di una particella.
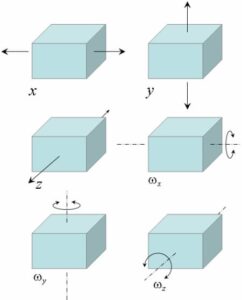
Per un atomo che si muove nello spazio tridimensionale, sono necessarie tre coordinate, quindi il grado libertà è pari a tre e ciò implica che il movimento dell’atomo è puramente traslazionale. Se la molecola è composta da N atomi il grado di libertà diventa 3N, perché ogni atomo ha 3 gradi di libertà.
Inoltre, poiché gli atomi sono legati tra loro i movimenti non sono solo traslazionali ma anche rotazionali, e vibrazionali. Per le molecole non lineari, tutti i movimenti rotazionali possono essere descritti in termini di rotazioni attorno a 3 assi e pertanto il grado di libertà rotazionale è 3 e i restanti 3N-6 gradi di libertà costituiscono movimento vibrazionale.
Per una molecola lineare, tuttavia, la rotazione attorno al proprio asse non è una rotazione perché lascia la molecola invariata. Quindi ci sono solo 2 gradi di libertà rotazionali per qualsiasi molecola lineare, lasciando 3N-5 gradi di libertà per la vibrazione.
Esempi di calcolo del numero di modi vibrazionali
Per calcolare il numero di modi vibrazionali di una molecola è quindi necessario conoscere, oltre al numero di atomi presenti, anche la sua geometria molecolare che può essere determinata tramite la teoria VSEPR. Per una molecola lineare sono presenti un numero di modi vibrazionali pari a 3N-5 mentre per una molecola non lineare il numero di modi vibrazionali pari a 3N-6

Per una molecola biatomica come, ad esempio, H2, O2, N2 ecc. il valore di N, ovvero degli atomi che la costituiscono, è pari a 2. La molecola è lineare pertanto il numero di modi vibrazionali è pari a (3 · 2) – 5 = 1.

Per una molecola lineare triatomica, come, ad esempio, biossido di carbonio, BeH2 e cianuro di idrogeno il numero N è pari a 3 quindi il numero di modi vibrazionali è pari a (3 · 3) – 5 = 4.
Per una molecola non lineare triatomica come, ad esempio H2O, ozono e anidride solforosa il numero N è pari a 3 quindi il numero di modi vibrazionali è pari a (3 · 3) – 6 = 3.



