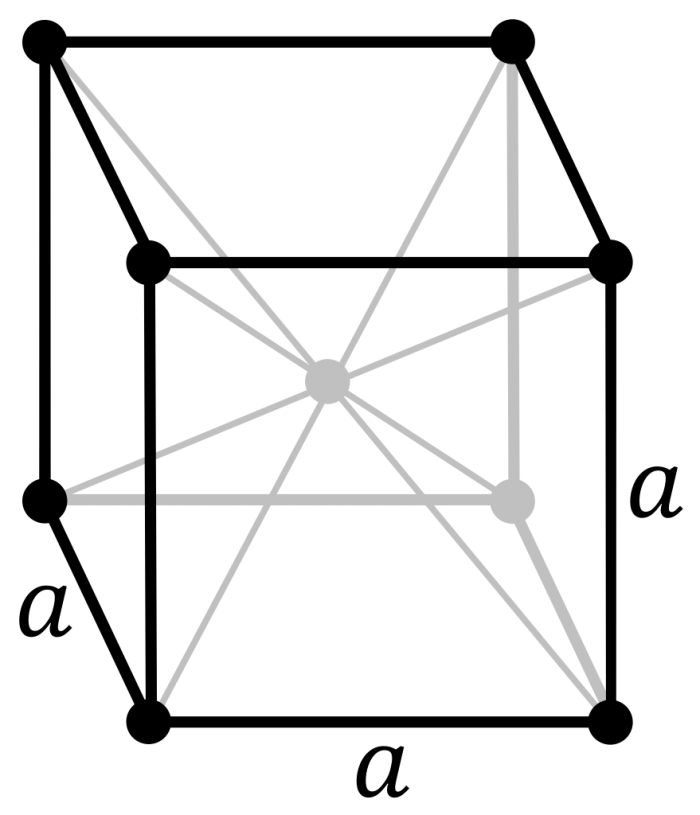
Il reticolo cubico a corpo centrato è uno dei reticoli di Bravais. Può essere considerato come un reticolo cubico semplice in cui è presente al centro una ulteriore unità. Pertanto, la cella unitaria di ciascun reticolo può essere considerata come due reticoli primitivi cubici semplici che si compenetrano.
Ciascuno degli otto punti reticolari all’angolo di una cella cubica è condiviso da otto celle cubiche adiacenti, mentre il punto reticolare al centro della cella cubica appartiene esclusivamente a quella cella.
Molti metalli tra cui cromo, ferro, molibdeno, potassio, sodio, tantalio, tungsteno e vanadio cristallizzano secondo un reticolo cubico a corpo centrato.
La cella unitaria di un reticolo cubico a corpo centrato (BCC) è costituita da un cubo ai cui vertici vi sono 8 atomi, molecole o ioni e uno al centro.
Struttura
Assumendo che le specie presenti siano assimilabili a una sfera rigida si può notare che la sfera centrale è circondata da 8 sfere quindi il numero di coordinazione ovvero il numero di sfere con i quali una data sfera è in contatto è pari a 8.
Poiché le sfere presenti ai vertici sono condivise con 8 celle unitarie adiacenti si può ritenere che solo 1/8 di ogni sfera appartenga ad una data cella unitaria.
Quindi le otto sfere presenti ai vertici nel loro insieme contribuiscono nel loro insieme all’equivalente di una sfera pertanto il numero di sfere per ogni cella unitaria è pari a 1+ (8∙ 1/8) = 2
Nel reticolo cubico a corpo centrato le sfere sono in contatto tra loro lungo la diagonale del cubo e si può trovare la relazione tra il lato del cubo e il raggio atomico.
Detto a il lato del cubo si può trovare la diagonale b del quadrato dal teorema di Pitagora:
b2 = a2 + a2 = 2 a2
da cui b = √2 a
Si consideri ora il triangolo rettangolo AFD di cui sono noti AD = a e DF = b = √2 a
Si può ottenere l’ipotenusa DF che chiamiamo c del triangolo tenendo conto che: c2 = a2 + b2 = a2 + (√2 a)2 = a2 + 2 a2 = 3 a2
Pertanto c = √3 a
Poiché lungo c si allineano 1 sfera e 2 mezze sfere ciascuna di raggio r si ha che c = 2r + r + r = 4r si ha
4r = c = √3 a (1)
Da cui r che rappresenta il raggio atomico è dato da:
r = √3 a/4
Fattore di impacchettamento atomico
Il fattore di impacchettamento atomico APF ovvero la frazione del volume della struttura cristallina occupata dagli atomi è dato dalla formula:
APF = Natomi Vatomo/ Vcella unitaria
essendo Natomi il numero di atomi presenti nella cella unitaria, Vatomo il volume di ogni atomo e Vcella unitaria il volume occupato dalla cella unitaria.
Nel caso di un reticolo cubico a corpo centrato il numero di atomi presenti nella cella unitaria è pari a 2.
Tenendo conto che il volume di una sfera è pari a V = 4 π r3/ 3 e che dalla (1) a = 4r/√3 si ha:
Natomi Vatomo : 2 ∙ 4 ∙π∙ r3/3 = 8 ∙π∙ r3/3
Il volume della cella unitaria è dato da:
Vcella unitaria = a3 = (4r/√3)3
Il fattore di impacchettamento atomico è quindi:
Natomi Vatomo/ Vcella unitaria = 8 ∙π∙ r3/3 / (4r/√3)3 = (8 ∙π∙ r3/3) ( √3/4r)3 = π(√3)3/24 = 0.680