Equazioni di Maxwell: il fondamento dell’elettromagnetismo
Le equazioni di Maxwell sono un insieme di quattro equazioni, ciascuna delle quali rappresenta rispettivamente un fenomeno, fondamentali dell’elettromagnetismo, formulate dal fisico scozzese James Clerk Maxwell nel 1861 e 1862. Le equazioni di Maxwell rappresentano un metodo efficace e conciso per enunciare i fondamenti dell’elettricità e del magnetismo.
Le equazioni di Maxwell infatti non furono enunciate da Maxwell, ma si deve a lui la capacità di combinare quattro equazioni fatte rispettivamente da Johann Friedrich Carl Gauss per il campo elettrico e per il campo magnetico, Michael Faraday per il campo magnetico variabile e André-Marie Ampère. Maxwell completò la quarta delle quattro equazioni, dovuta ad Ampere che pertanto prende il nome di equazione di Maxwell-Ampere ed è relativa al campo elettrico variabile.
La combinazione delle equazioni 3 e 4 può spiegare come un’onda elettromagnetica come la luce può propagarsi da sola. Le equazioni 3 e 4 rendono conto di come un campo magnetico variabile produca un campo elettrico variabile, che, a sua volta produce un altro campo magnetico variabile da cui e si forma un’onda elettromagnetica che si propaga nello spazio.
Le equazioni di Maxwell possono essere espresse in due forme ovvero in forma di equazioni integrali o in forma di equazioni differenziali. Le equazioni di Maxwell costituiscono una delle più grandi conquiste della fisica del diciannovesimo secolo e correlano la corrente elettrica al magnetismo.
Le quattro equazioni di Maxwell
Legge di Gauss per il campo elettrico
La legge di Gauss per il campo elettrico, pubblicata postuma nel 1867, descrive il campo elettrico statico generato da una distribuzione di cariche elettriche. Secondo questa legge, che è la prima delle equazioni di Maxwell, il flusso elettrico attraverso qualsiasi superficie chiusa è proporzionale alla carica elettrica totale racchiusa da questa superficie dove, per convenzione, una carica elettrica positiva genera un campo elettrico positivo.
In forma integrale viene espressa come:

dove E è il vettore del campo elettrico
il simbolo° indica il prodotto vettoriale della componente di E nella direzione di n dove n è il vettore normale unitario normale alla superficie
q è la quantità di carica elettrica contenuta nel volume
ε0 è la costante dielettrica nel vuoto
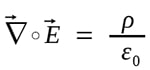
La legge di Gauss per il campo elettrico di Gauss per il campo elettrico può essere espressa in forma differenziale come
dove con ρ si è indicata la densità della carica distribuita uniformemente in tutto il corpo
Legge di Gauss per i campi magnetici statici
La legge di Gauss per i campi magnetici statici è la seconda delle equazioni di Maxwell ed è un’applicazione fisica del teorema di Gauss noto anche come teorema della divergenza.
In forma integrale è espressa come:
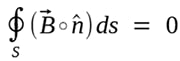
dove B è il flusso magnetico totale. Secondo la legge di Gauss per i campi magnetici statici è chiamata anche assenza di poli magnetici liberi il flusso magnetico totale attraverso una superficie chiusa è uguale a zero.
Ciò significa che il numero di linee di campo magnetico che entrano ed escono attraverso la superficie chiusa è la stessa.

La legge di Gauss per i campi magnetici nella forma differenziale può essere derivata usando il teorema della divergenza.
La legge di Gauss per i campi magnetici statici può anche essere derivata utilizzando la legge di Biot-Savart.
Legge dell’induzione di Faraday
La legge dell’induzione di Faraday è la terza delle equazioni di Maxwell e descrive il fenomeno dell’induzione elettromagnetica che si verifica quando il flusso del campo magnetico attraverso la superficie delimitata da un circuito elettrico è variabile nel tempo.

Essa prevede come un campo magnetico interagisce con un circuito elettrico per produrre una forza elettromotrice e, in forma integrale può essere espressa come:
Pertanto il cambiamento del flusso magnetico attraverso una superficie induce una forza elettromotrice in qualsiasi percorso di confine di quella superficie. La tensione accumulata attorno a un circuito chiuso è proporzionale alla velocità di variazione temporale del flusso magnetico che racchiude. Costituisce il principio di funzionamento di trasformatori , induttori, molti tipi di motori elettrici , generatori e solenoidi.

La legge dell’induzione di Faraday in forma differenziale è espressa da un’equazione in cui si evidenzia che un campo elettrico circolante è prodotto da un campo magnetico che cambia nel tempo. La direzione in cui fluisce la corrente è sempre tale da opporsi al cambiamento di flusso che l’ha prodotta.
Legge di Ampere-Maxwell
La legge di Ampere-Maxwell è l’ultima delle equazioni di Maxwell e mette in relazione correnti elettriche e flusso magnetico.

Secondo la legge di Ampere-Maxwell una corrente elettrica I o un flusso elettrico variabile attraverso una superficie produce un campo magnetico circolante attorno a qualsiasi percorso che delimita quella superficie. Il primo termine dovuto ad Ampere mostra la relazione tra una corrente Ienclosed e la circolazione del campo magnetico attorno a qualsiasi linea di contorno chiusa.
Il secondo termine dell’equazione è dovuta al contributo di Maxwell e mostra che la circolazione del campo magnetico è causata anche da una velocità di variazione temporale del flusso elettrico.
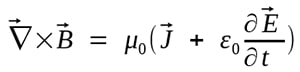
La legge di Ampere-Maxwell in forma differenziale mostra che un campo magnetico circolante è prodotto da una corrente elettrica e da un campo elettrico che cambia nel tempo.



