5 esercizi sui circuiti in parallelo

Si propongono 5 esercizi sui circuiti in parallelo ovvero circuiti in cui i carichi nei sistemi di distribuzione dell’energia sono per lo più collegati in parallelo.

I circuiti in parallelo sono costruiti collegando i terminali di tutti i singoli dispositivi di carico in modo che sia presente su ciascun componente lo stesso valore di tensione. Contrariamente ai circuiti in serie in un vi sono rami che forniscono più percorsi per il flusso della corrente.  I componenti si dicono  in parallelo se condividono due nodi

Per risolvere gli esercizi sui circuiti in parallelo bisogna conoscere la resistenza, la tensione e la corrente che fluisce. La tensione totale di un circuito parallelo ha lo stesso valore della tensione su ciascun ramo. Pertanto:
V = V₁= V₂ = V₃

Un circuito in  parallelo ha più di un percorso per il flusso di corrente. Il numero di percorsi di corrente è determinato dal numero di resistenze collegate in parallelo.

La corrente totale in un circuito in parallelo è la somma delle singole correnti di derivazione. Questa relazione in un circuito parallelo è espressa come:
i = i₁ + i₂ + i₃ +…

Per risolvere la corrente totale, si devono prima determinare le singole correnti di ramo usando la legge di Ohm, dovuta al fisico tedesco Georg Ohm
i_n = V/R_n

Resistenza

Se più resistenze sono collegate in parallelo si ha, come effetto, la riduzione della resistenza complessiva del circuito. La resistenza netta di un circuito in parallelo è sempre inferiore a qualsiasi valore di resistenza individuale.

Per la legge di Ohm dovuta
i₁ = V/R₁
i₂ = V/R₂
i₃ = V/R₃

Sostituendo queste espressioni nell’espressione della corrente totale i = i₁ + i₂ + i₃ +… si ha:
i = V/R₁+ V/R₂+ V/R₃
Da cui mettendo V in evidenza:
i = V(1/R₁+ 1/R₂+ 1/R₃)

Da cui V = i/(1/R₁+ 1/R₂+ 1/R₃)
La resistenza complessiva è comunemente determinata utilizzando l’equazione

1/R = 1/R₁ + 1/R₂ + 1/R₃ +…

Pertanto per i resistori in parallelo, la resistenza complessiva è il reciproco della somma dei reciproci dei singoli resistori. L’equazione precedente suggerisce che possiamo definire un nuovo resistore, equivalente ai resistori paralleli. Il nuovo resistore è equivalente nel senso che, per una data corrente i è presente la stessa tensione e R equivalente è dato da:

R = 1/(1/R₁ + 1/R₂ + 1/R₃)

Pertanto 1/R = 1/R₁ + 1/R₂ + 1/R₃

 5 esercizi sui circuiti in parallelo svolti

• Identificare, nel circuito indicato, quali sono le resistenze collegate in parallelo

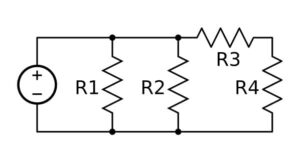
Due resistenze sono in parallelo quando gli estremi di entrata e gli estremi di uscita sono collegati fra loro ossia non si trovano sullo stesso filo in sequenza, ma sono collocate su più fili che si raccordano al circuito in nodi.

Pertanto le resistenze in parallelo nel circuito indicato sono R₁ e R₂

• Calcolare la resistenza equivalente del circuito rappresentato in figura:

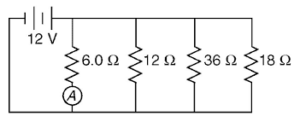
1/R = 1/R₁ + 1/R₂ + 1/R₃ + 1/R₄ = 1/6 + 1/12 + 1/36+ 1/18 = 12/36

Pertanto R = 36/12 = 3 Ω

• Una resistenza da 3.0 ohm, una sconosciuta, R, e due amperometri, A₁ e A₂, sono collegati come mostrato di seguito con una tensione di 12 volt. Determinare la resistenza equivalente sapendo che l’amperometro A₂ è attraversato da una corrente di 5.0 ampere.

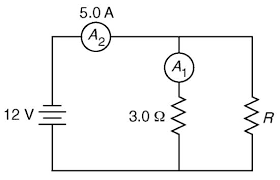
Per la legge di Ohm: V = iR
sostituendo i valori noti 12 =5 R
da cui R = 12/5 = 2.4 Ω

• Nel circuito in parallelo mostrato in figura in cui la tensione è pari a 5 V sono presenti tre resistenze: la resistenza R₁ è pari a 200 Ω, la resistenza R₂, attraversata da una corrente di 50 mA, è incognita e la resistenza R₃ è di 500 Ω. Determinare R₂, la corrente che attraversa le tre resistenze e la resistenza equivalente

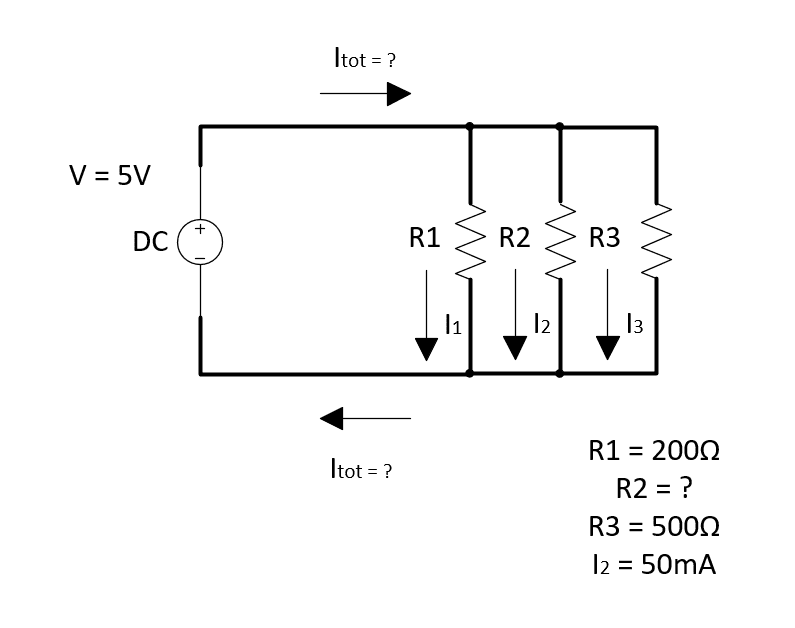
Dalla legge di Ohm R₂ = V/i = 5 V/0.050 A = 100 Ω
Applicando la formula i= V/R si ha:
i₁ = 5/200 = 0.025 A
i₃ = 5/500 = 0.010 A

La corrente totale i è data dalla somma di i₁, i₂ e i₃  da cui i = 0.025 + 0.050 + 0.010 = 0.085 A

R = V/i = 5 V/0.085 A =58.8 Ω

• Calcolare i dati mancanti del circuito rappresentato in figura

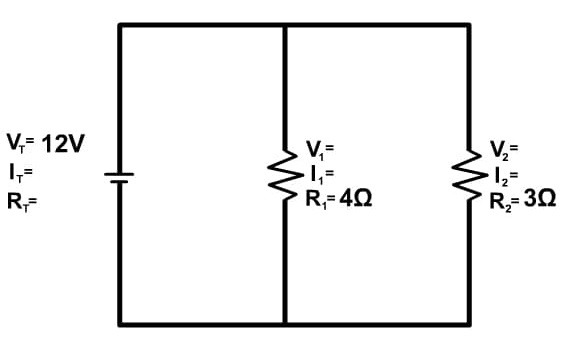
La tensione è uguale in ciascun ramo del circuito pertanto V_T = V₁ = V₂ = 12 V
Conoscendo V₁ e R₁ si può calcolare i₁:
i₁ = V/R₁ = 12 V/ 4 Ω = 3 A

Conoscendo V₂ e R₂ si può calcolare i₂:
i₂ = V/R₂ = 12 V/ 3 Ω = 4 A

La corrente totale i è data dalla somma di i₁ e i₂:
i = 3 A + 4 A = 7 A

La resistenza equivalente R è data da V/i:
R = 12 V/ 7 A = 1.7 Ω