6 esercizi sul principio di Archimede
Si propongono 6 esercizi sul principio di Archimede che è relativo al comportamento di un corpo immerso in un fluido ovvero un liquido o un gas. Secondo questo principio esposto da uno dei più grandi scienziati della storia “un corpo immerso in un fluido, riceve una spinta dal basso verso l’alto pari al peso del liquido spostato”
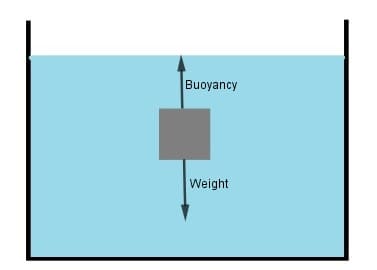
Sul corpo agisce quindi oltre alla sua forza peso anche una forza verticale orientata dal basso verso l’alto. Per risolvere gli esercizi sul principio di Archimede è necessario conoscere le formule relative.
Secondo il principio di Archimede la forza diretta verso l’alto indicata con FA e detta anche forza di galleggiamento è pari a:
FA = dflu · g · V
Dove dflu è la densità del fluido, g è l’accelerazione di gravità e V è il volume di fluido spostato
La forza peso
Fp = dsol · g · V
dove dsol è la densità del solido
Spinta di Archimede
La forza diretta verso l’alto, detta spinta di Archimede, è responsabile del galleggiamento dei corpi nei fluidi. Infatti se il peso del fluido spostato dal corpo immerso è maggiore del suo peso il corpo emergerà tanto da eguagliare la spinta di Archimede.
Possono verificarsi tre casi:
Se dsol > dflu si verifica che FA< Fp il corpo affonda
Se dsol = dflu si verifica che FA=Fp il corpo è in equilibrio. Ciò implica che, secondo la prima legge di Newton, se il corpo è in stato di quiete rimane in quiete mentre se in moto si muove di moto decelerato fino a fermarsi per effetto dell’attrito.
Se la densità del corpo è minore di quella del fluido il peso ovvero dsol < dflu si ha che FA> Fp il corpo tende a risalire fino alla superficie e quindi galleggia
In quest’ultimo caso si verifica che il volume immerso Vi sarà tale da spostare un volume di fluido che equilibri il peso del corpo. Pertanto
dflu · g · Vi = dsol · g · V
ovvero
dflu · Vi = dsol · V
da cui
Vi/V = dsol/dflu
6 esercizi sul principio di Archimede
- Determinare la densità di una palla di massa 4.0 kg che viene lasciata cadere in una vasca con fondo di 1.0 m2 e, dopo che è scesa sul fondo, l’acqua risale 2.5 mm
Il volume spostato è uguale al volume della palla: V = 1.0 m2 · 0.0025 m = 0.0025 m3
La densità della palla è pari a d = m/V = 4.0 kg/ 0.0025 m3 = 1600 kg/m3
- Una palla sferica di densità pari a 0.70 kg/L ha un raggio di r = 10 cm. Calcolare quanta parte della palla rimane immersa nell’acqua se viene posizionata sulla superficie dell’acqua e rilasciata supponendo che la densità dell’acqua sia pari a 1.0 kg/L
Il volume della palla è pari a V = 4 π r3/3 = 4 · 3.14 (10)3/3 = 4189 cm3 = 4.189 dm3 = 4.189 L
Dalla densità si può calcolare la massa della palla che è pari a m = d·V = 0.70 kg/L · 4.189 L = 2.9 kg che è pari alla massa di acqua spostata. Pertanto il volume di acqua spostata è pari a V = m/d = 2.9 kg/1.0 kg/L = 2.9 L
- Calcolare la forza di galleggiamento di 1.00 10 7 kg di acciaio completamente immerso nell’acqua sapendo che la densità dell’acciaio è 7.8 · 103 kg/m3 e quella dell’acqua è 1.0 kg/m3
Per trovare la forza di galleggiamento si deve trovare il peso dell’acqua spostata. Il volume dell’acciaio è pari a V = 1.00 · 10 7 kg/7.8 · 103 kg/m3 = 1.3· 106 m3.
Poiché l’acciaio è completamente sommerso, questo è anche il volume dell’acqua spostata. Ora si può trovare la massa d’acqua spostata dal rapporto tra il suo volume e la sua densità, entrambi noti.
m = 1.0 kg/m3 · 1.3· 106 m3 = 1.3· 106 kg
Per il principio di Archimede la forza di galleggiamento è F = mg = 1.3· 106 kg · 9.8 m/s2 = 1.3 · 107 N
- Calcolare quale frazione del volume totale di un iceberg emerge dall’acqua sapendo che la densità del ghiaccio è 0.92 g/cm3 e quella dell’acqua di mare è 1.03 g/cm3

La forza peso del ghiaccio è pari a Fp = dsol · g · V. Il peso del volume di acqua spostata dà la forza a questa spinta ma, poiché l’iceberg è in equilibrio si ha:
Vi/V = dsol/dflu = 0.92/1.03 = 89 %
Il volume dell’acqua spostata è il volume della parte immersa dell’iceberg quindi l’11% in volume dell’iceberg emerge
- Un cubo ha una massa di 2.33 kg. Calcolare la lunghezza minima del lato del cubo, secondo il principio di Archimede, perché esso galleggi nell’acqua di mare avente densità 1025 kg/m3
Si deve verificare che la forza peso del cubo sia pari alla spinta di Archimede ovvero:
Fp = FA
Quindi:
m·g = dflu · g · V = dflu · g · L3
dove L è il lato del cubo
da cui:
m = dflu · L3
pertanto L = ∛m/ dflu = 2.33/1025 = 0.131 m
- Un cubo di ferro con lato lungo 25.0 cm è immerso in una vasca piena di acqua a una temperatura 4 °C in modo tale che il fondo del cubo sia 1.00 m sotto la superficie dell’acqua. Calcolare la forza di galleggiamento sul cubo di ferro sapendo che a 4°C la densità dell’acqua vale 1.00 kg/m3. Calcolare inoltre qual è la forza minima richiesta per mantenere il cubo in equilibrio mentre rimane nell’acqua sapendo che la densità del ferro è 7.860 kg/m3
Il volume del cubo V è pari a V = (25.0 cm)3 = 1.56 ·104 cm3 = 0.0156 m3
Questo è lo stesso volume spostato dall’acqua. La forza di galleggiamento è pari a:
FA = m · g = dflu · g · V = (1.00 kg/m3) (0.0156 m3) ( 9.81 m/s2) = 0.1533 N ovvero, tenendo conto delle cifre significative, la forza di galleggiamento è pari a 0.153 N.
La forza normale è uguale alla differenza tra la forza di galleggiamento e il peso del cubo e, poiché il corpo è in equilibrio, si ha che Σ F = 0 ovvero FN + FA – mg = 0 da cui:
FN = – FA + mg
Una forza uguale alla forza normale FN applicata al cubo manterrà il cubo in equilibrio e sotto la superficie dell’acqua. Il peso del blocco di ferro è:
mferro ·g = dferro·V· g= (7.860 kg/m3) (0.0156 m3) ( 9.81 m/s2) = 1.21 N
Pertanto FN = – FA + mg = – 0.153 N + 1.21 N = 1.06 N



