Equazioni del moto di un fluido

Per ottenere  le equazioni che regolano il moto di un fluido si ricorre a un modello teorico di fluido ideale supposto del tutto incomprimibile e non viscoso essendo la viscosità è una misura dell’attrito interno in un fluido.

Una massa fluida in movimento può essere trattata come un mezzo continuo in ogni punto del quale è definito il vettore velocità. In regime stazionario lo stato fisico e la velocità in ogni punto fisso rispetto a un sistema di riferimento non variano con il tempo.

Consideriamo il moto stazionario di un fluido fra due lastre piane in modo tale che solo la componente lungo l’asse x differisca da zero cioè u_y e u_z  sono entrambe nulle e che la u_x dipenda solo dalla posizione lungo l’asse z cioè u_z = f(z). Si assume che il fluido sia incomprimibile e che la sua resistenza interna τ sia esprimibile tramite la legge di Newton. Le equazioni del moto di un fluido si scrivono isolando un elemento di volume dxdydz = dV e uguagliando la forza di inerzia ( massa per accelerazione ) alla somma delle forze a esso applicate.

Forza di inerzia

La forza di inerzia F.I. sarà espressa da:

F.I. = dm du_x/dt = dm ( ∂u_x /∂z  + u_x ∂u_x/ ∂z)

In realtà, essendo il moto stazionario ∂u_x / ∂t =0 ed inoltre dm = ρdV

Le forze esterne sono invece dovute alla pressione, all’attrito interno esistente nel fluido e all’azione di un campo esterno, per esempio quello gravitazionale. Se il moto è orizzontale l’ultimo termine può essere omesso.

Forze dovute alla pressione F.E.N

Le forze dovute alla pressione F.E.N. agiscono su facce parallele e la loro risultante è espressa da:

F.E.N. = P dydz – (P + ∂P/∂x dx) dydz = – ∂P/∂x dV

Le forze di attrito F.E.T. agiscono tangenzialmente rispetto alle facce a e b e la loro risultante è espressa da:

F.E.T. = – ( τ + ∂τ/∂z dz) dxdy + τ dxdy = – dτ/dz dV

Uguagliando la somma F.E.N + F.E.T a F.I. con opportune semplificazioni l’equazione del moto diviene:

ρ u_z du_x/dz = – ∂P/∂x – ∂τ/∂x

dove ρ u_z du_x/dz è il termine inerziale; ∂P/∂x è il termine dovuto alla pressione e ∂τ/∂x è il termine dovuto all’attrito interno. In realtà essendo u_z = 0 l’equazione precedente si semplifica come segue:

∂P/∂x = – ∂τ/∂x

Esprimendo le forze tangenziali secondo l’equazione τ = – μ ∂u_x/ ∂z si ha:

∂P/∂x = μ ∂² u_x/ ∂z²

Integrando quest’ultima equazione si ha:

μu_x = ∂P/∂x (z²/2) + C_1z + C₂

C₁ e C₂ sono due costanti di integrazione i cui valori possono essere valutati applicando le seguenti condizioni al contorno:

u_x = 0 per z = z_w , z = – z_w

esse implicano che non esista scorrimento del fluido in corrispondenza delle pareti ( z_n , – z_n).  Si ricava:

u_x = – 1 / 2μ ∂P/∂x (z²_w – z²)

ciò indica che il profilo di velocità è parabolico. Tale risultato costituisce una peculiarità dei moti viscosi o laminari nei quali le forze di attrito interne al fluido si possono esprimere mediante l’equazione di Newton τ = – μ ∂u_x/ ∂z.

Modi per rappresentare il moto di un fluido

I vettori di velocità vengono spesso utilizzati per illustrare il moto di un fluido in applicazioni come la meteorologia. Ad esempio, il vento – il movimento fluido dell’aria nell’atmosfera – può essere rappresentato da vettori che indicano la velocità e la direzione del vento in un dato punto su una mappa.

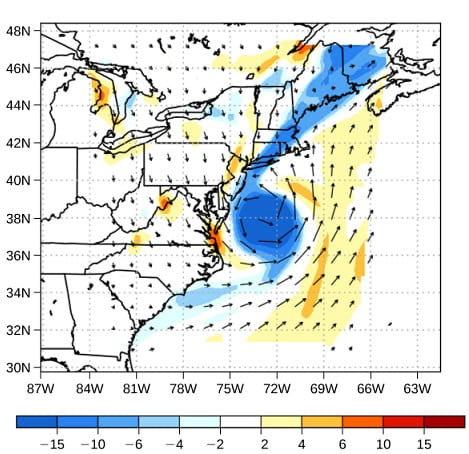
La figura mostra i vettori di velocità che descrivono i venti durante l’uragano Arthur nel 2014. Un altro metodo per rappresentare il moto di un fluido è una linea di flusso . Una linea aerodinamica rappresenta il percorso di un piccolo volume di fluido mentre scorre. La velocità è sempre tangente alla linea di flusso.

I diagrammi in utilizzano le linee di flusso per illustrare due esempi di fluidi che si muovono attraverso un tubo. Il primo fluido presenta un flusso laminare (a volte descritto come flusso costante), rappresentato da linee di flusso lisce e parallele. Si noti che nell’esempio mostrato nella parte (a), la velocità del fluido è maggiore

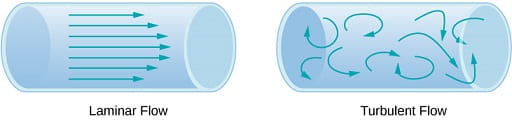
al centro e diminuisce vicino alle pareti del tubo a causa della viscosità del fluido e dell’attrito tra le pareti del tubo e il fluido.

Questo è un caso speciale di flusso laminare , dove l’attrito tra il tubo e il fluido è elevato, noto come condizioni al contorno di non scorrimento. Il secondo diagramma rappresenta il flusso turbolento, in cui le linee di flusso sono irregolari e cambiano nel tempo. Nel flusso turbolento , i percorsi del flusso del fluido sono irregolari poiché diverse parti del fluido si mescolano insieme o formano piccole regioni circolari che assomigliano a vortici. Ciò può verificarsi quando la velocità del fluido raggiunge una certa velocità critica.