L’effetto Stark è lo spostamento dei livelli di energia atomica causato da un campo elettrico esterno. Ciò causa la separazione delle linee spettrali di atomi e molecole.
È analogo all’effetto Zeeman che consiste nella separazione delle linee spettrali a causa di un campo magnetico esterno.
È detto del primo o del secondo ordine a seconda che l’entità del fenomeno vari linearmente oppure in modo quadratico al variare del campo elettrico applicato.
Il fisico tedesco Johannes Stark nel 1913 osservò per la prima volta per l’atomo di idrogeno e può essere osservato sia per le righe di emissione che per quelle di assorbimento.
Indipendentemente da Stark il fisico italiano Antonino Lo Surdo scoprì lo stesso effetto lo stesso anno e pertanto è spesso denominato effetto Stark-Lo Surdo. Per questa scoperta Stark vinse il Premio Nobel per la Fisica nel 1919.
Atomo di idrogeno e effetto Stark
Per comprendere il fenomeno si applica la teoria delle perturbazioni che comprende metodi per trovare una soluzione approssimativa di un problema, partendo dalla soluzione esatta di un problema correlato e più semplice e aggiungere all’operatore hamiltoniano un termine perturbativo, che rappresenti un disturbo del sistema.
L’effetto può essere osservato come un possibile spostamento del livello di energia, quando si applica un campo elettrico esterno all’atomo di idrogeno.
L’atomo di idrogeno ha un momento di dipolo elettrico dovuto alla carica positiva del protone e alla carica negativa dell’elettrone.
Esse sono separate da una distanza che è dell’ordine del raggio di Bohr.
Quando è applicato un campo elettrico esterno a un atomo di idrogeno, la perturbazione hamiltoniana è data dal prodotto scalare tra il momento di dipolo elettrico e campo elettrico
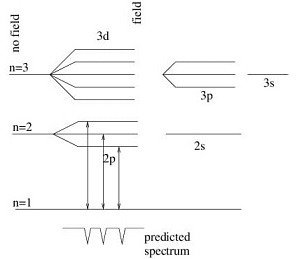
In assenza di campo elettrico il livello di energia dipende dal numero quantico principale n:
E°n = – n/R2 dove R = 13.605693122994 eV
Lo stato fondamentale con n = 1 ( l= 0 e m =0) è non degenere.
Il primo stato eccitato con n = 2 (l=1 e m=1,0,-1) presenta 22 = 4 gradi di degenerazione
Il secondo stato eccitato con n = 3 (l= 2, m = 2,1,0,-1,-2 e l = 1, m= 1,0,-1). Esso presenta 32= 9 gradi di degenerazione
Per valutare lo shift dei livelli energetici in presenza di un campo elettrico si applica la teoria delle perturbazioni allo stato fondamentale e agli stati eccitati.
È necessario quindi valutare la variazione della densità di probabilità della funzione d’onda dell’atomo di idrogeno quando è applicato il campo elettrico. Ci si aspetta che la densità di probabilità varia in funzione della grandezza e della direzione del campo elettrico
Spettri atomici
La scissione dei livelli di energia da parte di un campo elettrico richiede prima che il campo polarizzi l’atomo e quindi interagisca con il risultante momento di dipolo elettrico. Questo momento di dipolo dipende dalla grandezza di M j , ma non dal suo segno, cosicché i livelli di energia mostrano uno splitting proporzionale ai numeri quantici J+1 o J+1/2, rispettivamente per spin interi e semi interi.
L’effetto Stark è stato importante nell’analisi degli spettri atomici, ma soprattutto per gli spettri rotazionali molecolari per la misurazione delle energie di transizione tra stati rotazionali quantizzati di molecole in fase gassosa.
