Funzione gaussiana: espressione matematica, grafico
Le misure di una grandezza sono soggette a piccoli errori casuali esse si distribuiscono secondo una funzione gaussiana a forma campanulare. Il matematico tedesco Carl Friedrich Gauss nell’ambito dei suoi studi in tutti i campi scientifici propose per primo la funzione nel 1809 che prese il suo nome
L’espressione matematica della funzione gaussiana è:
f(x) = Ne-(x- μ)2/2σ2
dove N è una costante detta di normalizzazione, e σ è un parametro fisso detto parametro di larghezza della curva di Gauss. Quest’ultimo è infatti correlato alla larghezza della campana che è larga se σ è grande e stretta se σ è piccolo. Il valore di N è pari a 1/σ√2π e μ è la media
Condizione necessaria affinché la distribuzione rispetti la funzione gaussiana è che gli errori strumentali siano trascurabili.
Grafico della funzione
La funzione gaussiana è una distribuzione di probabilità continua simmetrica rispetto al massimo e quindi il lato destro del centro è un’immagine speculare del lato sinistro.
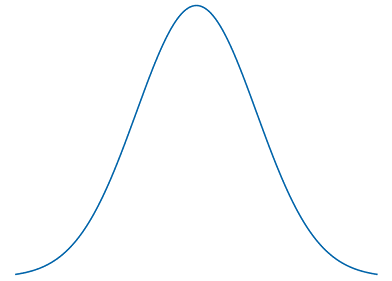
Poiché la funzione gaussiana ha lo stesso valore per valori positivi e per valori negativi della x, ovvero f(x) = f(-x) essa è una funzione pari.
La maggior parte dei valori di dati continui in una distribuzione normale tende a raggrupparsi attorno alla media e più un valore è lontano dalla media, meno è probabile che si verifichi. Le code sono asintotiche, il che significa che si avvicinano ma non incontrano mai l’asse delle ascisse
Per una distribuzione perfettamente normale la media, la mediana e la moda hanno lo stesso valore, rappresentato visivamente dal picco della curva.
L’area sotto la curva di distribuzione normale rappresenta la probabilità e l’area totale sotto la curva somma a uno.
Usi
La funzione gaussiana è utilizzata in ambito scientifico e in campo ingegneristico. In ambito statistico e della teoria della probabilità, è usata come funzione di densità di una distribuzione normale. In fisica, appare nell’oscillatore armonico quantistico, nella teoria quantistica dei campi, nell’ottica e in molte altre teorie e modelli.
Allo stesso modo, in chimica è usata per rappresentare gli orbitali molecolari. In informatica, le funzioni gaussiane sono utilizzate nell’elaborazione delle immagini.



