Distribuzione di Maxwell-Boltzman: grafico
La distribuzione di Maxwell-Boltzman è una funzione di distribuzione che dà la probabilità che una particella abbia velocità compresa tra v e v + e può essere espressa come
dvdN/N = 4 π ( M/2 π RT)3/2 v2 e-Mc2/2RT dv
dove N è il numero totale di molecole presenti, dN/N è la frazione di molecole che hanno una velocità compresa tra v e v+dv, M è il peso molecolare in Kg/mol, T la temperatura espressa in gradi Kelvin e R la costante dei gas che vale 8.31 J/ mol K.

Le particelle gassose hanno ciascuna un loro moto e quindi sono dotate di energia cinetica; tali particelle, tuttavia, a una determinata temperatura non hanno la stessa velocità e pertanto risulta impossibile poter prevedere la velocità di ciascuna particella in un determinato istante. Si deve pertanto ricorrere a metodi statistici per ottenere una funzione di distribuzione delle particelle con una certa velocità.
La distribuzione di Maxwell-Boltzman elaborata tra la metà e la fine del 1800 da James Clerk Maxwell e Ludwig Boltzmann consente di conoscere la distribuzione delle velocità in un gas a una certa temperatura
Curva della distribuzione di Maxwell-Boltzman
Ponendo sull’asse delle ordinate dN/N e su quella delle ascisse v si ottiene un grafico come quello rappresentato in figura. La curva è detta curva della distribuzione di Maxwell-Boltzman.
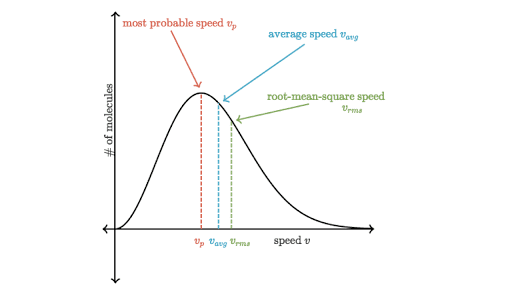
La curva non è simmetrica infatti c’è una “coda” più lunga all’estremità destra del grafico che corrisponde a una velocità elevata mentre a sinistra terminare a zero poiché una molecola non può avere una velocità inferiore a zero
Si può notare che solo una piccola frazione di molecole hanno una velocità molto alta o molto bassa; la velocità posseduta dalla massima frazione di molecole è detta velocità più probabile che aumenta con l’aumentare della temperatura in quanto un aumento di temperatura comporta un aumento del moto delle particelle.
Si può osservare che finché la temperatura di un gas è costante, la frazione avente la velocità pari alla velocità più probabile rimane la stessa, ma le molecole aventi questa velocità può non essere la stessa. Il picco della curva dà la velocità più probabile, ovvero la velocità posseduta dalla maggior parte delle molecole.
Si potrebbe ritenere che la velocità corrispondente al picco del grafico di Maxwell-Boltzmann sia la velocità media di una molecola nel gas. Invece questo valore corrisponde alla velocità più probabile. L’area totale sotto l’intera curva è uguale al numero totale di molecole nel gas.
Se si riscalda il gas a una temperatura più alta, il picco del grafico si sposterà verso destra poiché la velocità molecolare media aumenta. Man mano che il grafico si sposta verso destra, l’altezza del grafico deve diminuire per mantenere la stessa area totale sotto la curva. Allo stesso modo, quando un gas si raffredda a una temperatura inferiore, il picco del grafico si sposta a sinistra.
Velocità
Le molecole cambiano continuamente la loro velocità a causa delle collisioni pertanto i loro moti possono essere descritti in termini di differenti tipi di velocità molecolari:
1) Velocità più probabile
La velocità più probabile e quella posseduta dalla massima frazione di molecole gassose a una determinata temperatura e viene indicata con α dove
α = √ 2RT/M
2) Velocità media
La velocità media rappresenta una media aritmetica delle velocità posseduta dalle molecole di un campione di gas ed è definita come:
ṽ = v1 + v2 + … + vN/ N
Si può dimostrare che:
ṽ = √ 8 RT/π M
3) Radice della velocità quadratica media:
è espressa dalla relazione
ṽqm = √N1v12 + N2v12 + N3v32+ …/N1 + N2+ N3+ …
La radice della velocità quadratica media è data dalla relazione:
ṽqm = √3 RT/M
La velocità più probabile, la velocità media e la radice della velocità quadratica media stanno tra loro in rapporto di 1 : 0.9213 : 0.8177 quindi α > ṽ > ṽqm

