Processo isotermico: lavoro, grafici, esempi

Un processo isotermico avviene a temperatura costante e per esso vale la legge di Boyle dovuta a Robert Boyle per la quale il prodotto tra pressione e volume è costante:
pV = K

Consideriamo un sistema che passa dallo stato A caratterizzato dalla pressione p₁, dal volume V₁ e dalla temperatura T, allo stato B caratterizzato dalla pressione p₂, dal volume V₂ e dalla temperatura T. Dall’ equazione di stato dei gas:
p₁V₁ = nRT
p₂V₂ = nRT
da cui p₁V₁ = p₂V₂ = nRT

Lavoro in un processo isotermico

In una espansione isoterma reversibile il lavoro w compiuto dal sistema e avente pertanto segno negativo è dato da:

w = – ∫pdV essendo l’integrale definito tra V₁ e V₂.

In tale processo la pressione non è costante ma varia in funzione del volume. Sappiamo dall’equazione di stato dei gas che p = nRT/V

Sostituendo a p il suo valore nell’integrale si ha:

w = – ∫nRTdV/V essendo l’integrale definito tra V₁ e V₂

Essendo nRT costanti l’integrale si riduce a:

w = – nRT∫dV/V essendo l’integrale definito tra V₁ e V₂

Risolvendo l’integrale si ha:

w = – nRT(ln V₂-V₁) = – nRT ln(V₂/V₁)

Un processo isotermico può essere rappresentato dal seguente diagramma pV:

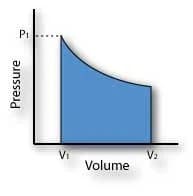
In un processo isotermico la variazione dell’energia interna è pari a zero e pertanto dal Primo principio delle termodinamica: ΔQ = Δw + ΔU si ottiene:

ΔQ = Δw

Il calore fornito durante tale processo viene usato per compiere lavoro contro l’ambiente esterno.

Esempio

Un campione costituito da 2.00 moli di He è fatto espandere isotermicamente alla temperatura di 295 K dal volume di 22.8 dm³ al volume di 31.7 dm³. Calcolare w e q se:

a)      La trasformazione avviene in modo reversibile

b)      La trasformazione avviene contro una pressione esterna uguale alla pressione finale del gas

Caso a)

Quando la trasformazione avviene in modo reversibile si ha p_est = p_sis

Pertanto w = – nRT ln(V₂/V₁) = – 2.00 mol ∙ (8.31447 J/mol K)(295 K) ln (31.7 dm³/22.8 dm³)= – 1.62 ∙ 10³ J = – 162 kJ

q = – w = + 162 kJ

Caso b)

La pressione finale p₂ è pari a:

p₂ = nRT/V₂ = 2.00 mol ( 0.08206 L atm/mol K) ( 295 K) / 31.7 L = 1.53 atm

poiché 1 atm = 101325 Pa

si ha p₂ = 1.55 x 10⁵ Pa

w = – p_est ΔV = – 1.55 ∙ 10⁵ ( 31.7 – 22.8) = – 1.38 ∙ 10⁶ J = – 1.38 ∙ 10³ kJ

q = – w = + 1.38 ∙ 10³ kJ

Per un processo isotermico pV = K

Differenziando l’equazione si ha:

pdV + Vdp = 0

ovvero pdV = – Vdp

da cui

p = – Vdp/dV

Il termine – Vdp/dV viene definito come modulo di compressibilità e misura la resistenza di una specie ad una compressione uniforme