Espansione adiabatica di un gas reale
L’equazione dell’espansione adiabatica di un gas ideale p1V1γ = p2V2γ non è valida per i gas reali. Joule e Thomson effettuarono un esperimento per valutare le proprietà dei gas reali a seguito di un’espansione. Un campione di gas alla pressione p1 , alla temperatura T1 che si trova in un volume V1 viene fatto passare attraverso un setto poroso a pressione costante.
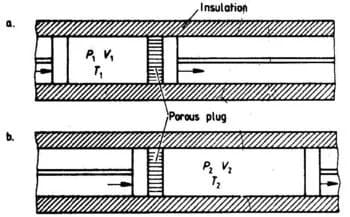
A seguito dell’espansione il gas ha una pressione p2, un volume V2 e una temperatura T2; essendo un processo che avviene in modo adiabatico q = 0.
Il lavoro fornito al gas sul lato sinistro del setto poroso è pari a p1V1 mentre quello svolto dal gas sul lato destro del setto poroso è – p2V2:
Il lavoro netto è pertanto:
W = p1V1 – p2V2
Espansione adiabatica di un gas reale e funzioni di stato
La variazione di energia interna ΔU = q + W vale quindi, tenendo conto che q = 0 e sostituendo a W il suo valore vale quindi:
ΔU = p1V1 – p2V2 ≠ 0
In questo processo, analogamente all’espansione di Joule, dal nome del fisico inglese James Joule, l’energia interna non rimane costante mentre l’entalpia definita come:
ΔH = ΔU + Δ(pV) sostituendo a ΔU il valore ricavato ed esplicitando il termine Δ(pV) vale:
ΔH = p1V1 – p2V2 + p2V2 – p1V1 = 0
Cosicché tale processo avviene senza variazione di entalpia e, per ogni valore di Δp si può misurare ΔT. Il rapporto tra queste due quantità vale:
ΔT/Δp ∼ (δT/δp)H = μJT
Dove μJT è detto coefficiente di Joule-Thomson. Il valore di tale coefficiente è diverso da zero per i gas reali mentre vale zero per i gas reali. Infatti:
(δT/δp)H = – (δH/δp)T/ (δH/δT)p = – (δH/δp)T/ Cp
Essendo Cp il calore specifico a pressione costante. Il numeratore della frazione è pari a zero per un gas ideale, ma non necessariamente per un gas reale.
Il valore di μJT dipende dal gas preso in esame, così come dalla temperatura e dalla pressione del gas prima dell’espansione. Per tutti i gas reali questo valore è uguale a 0 nel punto chiamato punto di inversione e la temperatura di inversione Joule-Thomson (Kelvin) è la temperatura alla quale il coefficiente cambia di segno.
Una espansione adiabatica reversibile, in cui il gas fa un lavoro positivo durante il processo di espansione, invece crea invariabilmente una diminuzione di temperatura.
Il valore di tale coefficiente è una funzione decrescente della temperatura e passa attraverso lo zero alla temperatura di inversione. In una espansione dp < 0 mentre dT può essere sia positivo che negativo a seconda del segno di μJT. Infatti essendo μJT = (δT/δp)H se esso assume un valore positivo allora dT è negativo nel corso dell’espansione e pertanto il gas si raffredda. Viceversa se μJT è negativo allora dT è positivo e il gas si riscalda durante l’espansione



